ALU nebo ve španělštině známé jako logikoaritmetická jednotka jsou jednotky v rámci Procesor (CPU) nebo GPU kteří jsou doslova zodpovědní za křupavá čísla, a proto jsou zodpovědní za všechny matematické výpočty, které se v našich počítačích provádějí několik miliardkrát za sekundu. Jak ale fungují, jaké typy existují a jaké jsou tajemství jednotek ALU? Čtěte dál a zjistěte to.
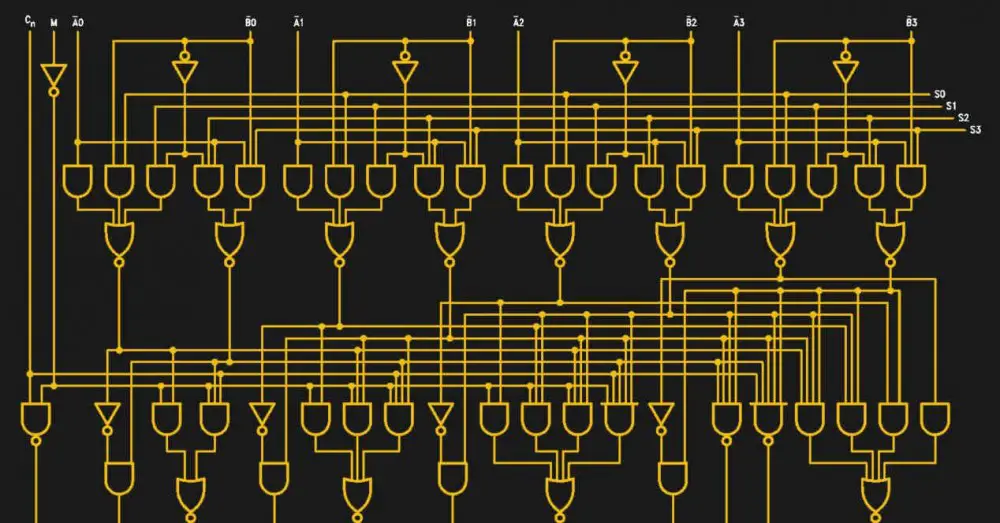
První ALU, která měla být vydána, nebyla součástí CPU, ale spíše čipem řady 7400 s rozhraním TTL od společnosti Texas Instruments, 74181 byla první ALU integrovaná do jediného čipu. Byl pouze 4bitový a používal se v různých minipočítačích během šedesátých let, což znamenalo první velký přechod ve výpočetní technice.
Konstrukce prvních kompletních CPU během 70. let a se všemi odpovídajícími prvky pro provedení kompletního instrukčního cyklu samozřejmě musela počítat s integrací ALU pro výpočet logických a aritmetických instrukcí uvnitř čipu.
Typy ALU
Můžeme rozdělit ALU na dvě různá dělení, první je podle typu čísla, které se má vypočítat, a proto, pokud je provozováno s celými čísly nebo s plovoucí desetinnou čárkou, kde ve druhém případě mluvíme o provozu s desetinnými místy. Operace s plovoucí desetinnou čárkou se řídí pravidlem, které označuje, kolik bitů čísla odpovídá celé části a kolik zlomkové části.
Standardy v obou případech také označují, zda první číslo označuje znaménko, či nikoli, například číslo v 8bitových celých číslech může představovat číslo od 0 do 255 nebo od -127 do 127 v závislosti na použitém formátu.
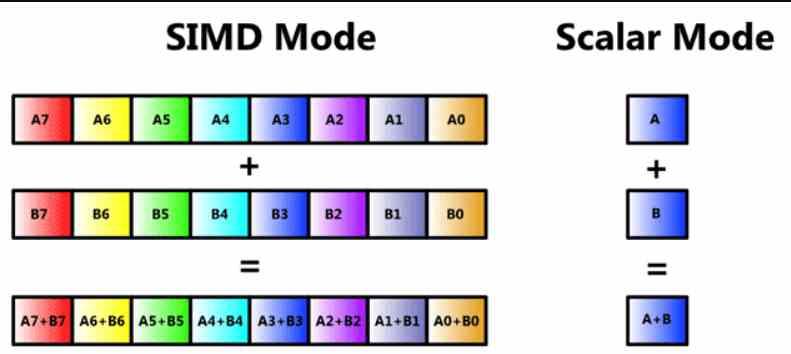
Druhá kategorizace odkazuje na to, kolik dat a pokynů ALU provede současně. Nejjednodušší formou je skalární ALU, kde operaci nebo instrukci provádí operand. Máme také SIMD nebo vektorové jednotky, které provádějí stejnou instrukci s různými operandy současně.
Druhy operací s ALU
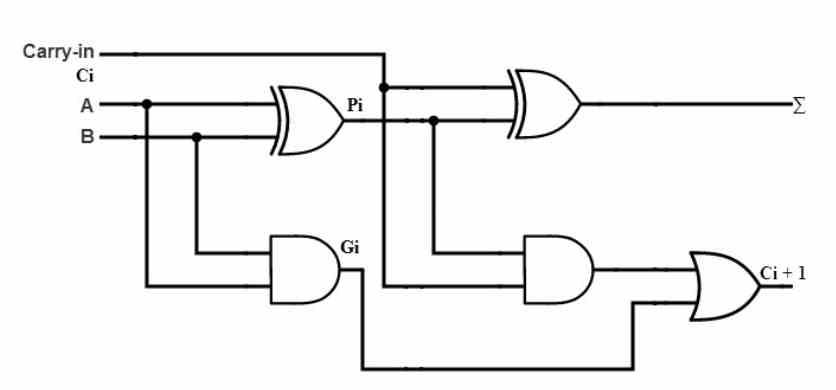
Nejprve musíme mít ALU, která sama o sobě nemůže fungovat, takže bude nutné uvést řídicí jednotku, která určí, kterou instrukci provést a na kterých datech ji provést. V tomto vysvětlení tedy předpokládáme, že máme řídicí jednotku doprovázející naši ALU.
ALU, která umožňuje libovolnému typu procesoru, ať už je to CPU nebo GPU, provádět matematické operace s binárními čísly. Nejde tedy o nic jiného než o binární kalkulačku, která je nejjednodušším typem ALU, která umožňuje přidání dvou čísel po 1 bitech, což je operace, která by vypadala následovně:
| Operace | Výsledek | nákladní doprava |
|---|---|---|
| 0 + 0 | 0 | 0 |
| 0 + 1 | 1 | 0 |
| 1 + 0 | 1 | 0 |
| 1 + 1 | 1 | 1 |
Pokud se podíváte na tyto, jedná se o specifikace logické brány typu OR, ale najdeme problém, který je třeba nést při přidávání 1 + 1, protože výsledek přidání binárního 1 + 1 je 10 a ne 1. Takže musíme vzít v úvahu, že 1 v přenášení, které přenášíme, a proto jednoduchá brána OR nestačí, zvláště pokud chceme pracovat s mnohem vyšší přesností v bitech, a proto máme mnohem složitější ALU v počtu bitů.
Binární odčítání v ALU
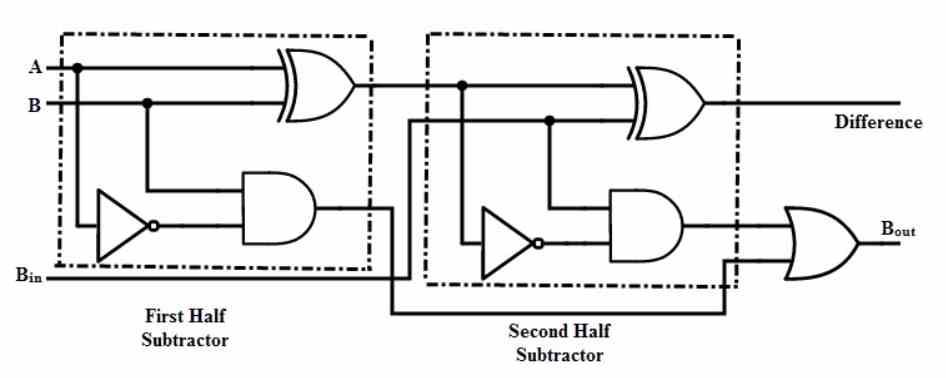
Odečtení nebo odčítání lze odvodit pomocí následujícího vzorce:
A - B = A + NE (B) +1
Trik je zde velmi jednoduchý, je založen na skutečnosti, že pracujeme s binárními celými čísly. To nefunguje s čísly s plovoucí desetinnou čárkou. Můžeme použít stejný mechanismus, který se používá k přidání dvou čísel k provedení operace odčítání. Jediné, co musíme udělat, je převrátit hodnotu druhého operujícího řadou NOT bran a přidat 1 ke konečnému výsledku. Díky nim můžeme použít stejný hardware k provedení operace přidání k provedení odečtení.
Binární násobení a dělení v mocninách 2
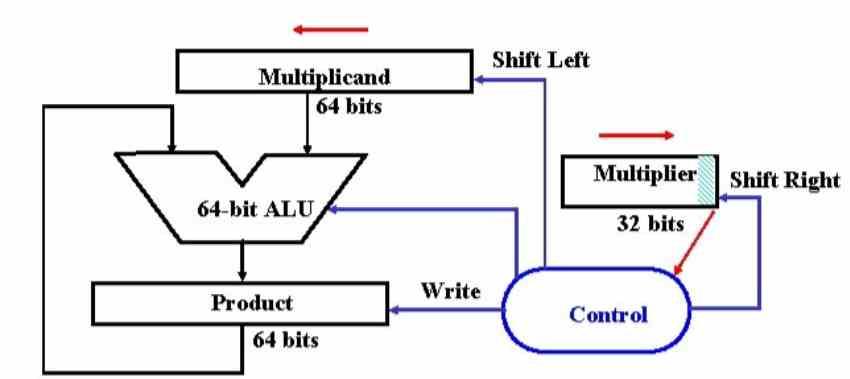
Nejjednodušší formou násobení v binárním systému je násobení čísly násobky 2, což je binární systém, musíme implementovat pouze mechanismus, kde jsou vstupní data posunuta o několik pozic doleva, pokud se násobíme, nebo doleva . správně, pokud rozdělujeme. Počet pozic? Závisí to na výkonovém indexu 2 multiplikátoru, takže pokud vynásobíme 8, což je 2 ^ 3, budeme muset posunout pozice číslo 3 doleva a pokud bude dělit 3 pozice doprava. Z tohoto důvodu ALU také integrují operace bitového posunu, které jsou základem pro násobení nebo dělení násobky 2.
Ale pokud mluvíme o znásobení jiných typů čísel, je nejlepší vrátit se zpět, když jsme byli ve škole malí.
Násobení bez síly 2 čísel
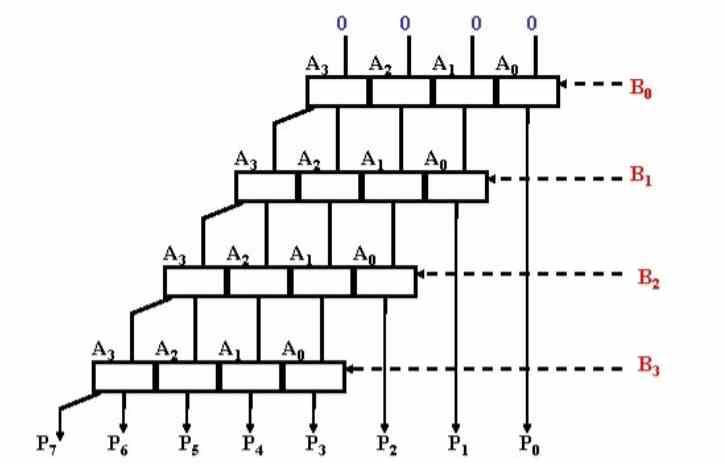
Po mnoho let byly ALU velmi jednoduché a mohly se jen přidávat, protože neměly ALU určené k násobení. Jak si tehdy vedli? Provedení několika zřetězených součtů, které jim trvalo mnoho cyklů. Jako historická kuriozita byl jedním z prvních domácích procesorů, které měly multiplikační jednotku Intel 8086.
Předpokládejme, že chceme znásobit 25 x 25, když jsme byli malí, to, co jsme udělali, bylo následující:
- Nejprve vynásobíme 25 x 5 a zapíšeme výsledek, což je 125.
- Za druhé vynásobíme 25 x 2, což nám dá 50 a zapíšeme výsledek, ale posuneme o jednu pozici doleva.
- Sčítáme obě čísla, protože máme druhé číslo posunuté doleva, výsledek součtu není 175, ale 625, což je výsledek vynásobení 25 x 25 v desítkové soustavě.
V binárním procesu je proces stejný, ale číslo 25 je v tomto případě 11001, a tedy 5bitové číslo. Takže binární budeme vynásobit 11001 x 11001 a k tomu budeme muset použít AND brány.
- Nejprve vynásobíme 11001 x 1 = 11001
- Za druhé, vynásobíme 11001 x 0 = 0000, výsledek zapíšeme o jedno místo vlevo.
- Třetí vynásobíme 11001 x 0 = 0000, výsledek zapíšeme o dvě místa vlevo.
- Za čtvrté, vynásobíme 11001 x 1 = 11001, výsledek zapíšeme o tři místa vlevo
- Za páté, vynásobíme 11001 x 1 = 11001, výsledek zapíšeme o čtyři místa vlevo
- S přihlédnutím k pozici každé operace přidáme výsledek, který by jako výsledek neměl dát 01001110001
Složitější matematické operace

S výše uvedeným vysvětlením můžete vytvářet jednotky k provádění mnohem složitějších matematických operací, jako jsou dělení, druhé odmocniny, moc atd. Složitější operace bude samozřejmě vyžadovat více tranzistorů. Ve skutečnosti pro každou operaci existuje jiný mechanismus a když řídicí jednotka řekne ALU typ operace, kterou má provést, pak to, co dělá, říká, že musí použít tento konkrétní mechanismus pro tuto konkrétní matematickou operaci.
Protože je důležité ušetřit na tranzistorech, nejsložitější operace jsou definovány jako posloupnost nejjednodušších za účelem opětovného použití hardwaru. To vede k složitějším operacím vyžadujícím vyšší počet hodinových cyklů. I když v některých návrzích jsou implementovány kompletní mechanismy, které umožňují tyto operace provádět v mnohem menším počtu cyklů a dokonce v jediném cyklu v mnoha případech, ale nejsou v CPU běžné.
Kde se používají v GPU, kde vidíme typ jednotky zvané Special Function Unit, která je zodpovědná za provádění toho, co nazýváme transcendentální operace, jako jsou trigonometrické poměry, které se používají v geometrii.
Kde získává ALU data k provozu?
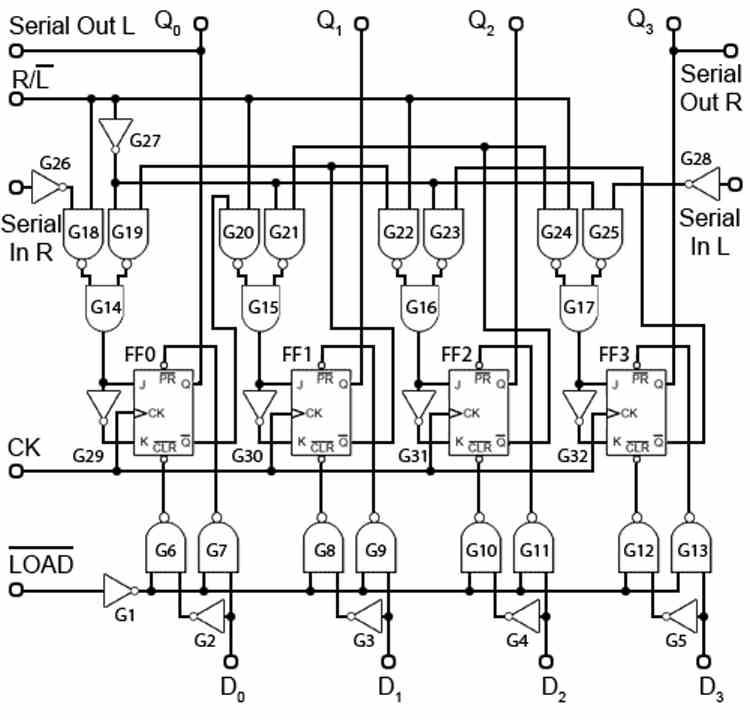
Nejprve musíme mít na paměti, že ALU nepracuje s daty v paměti, ale že v procesu snímání a dekódování dat, se kterými musí pracovat, je uložena v registru zvaném akumulátor, na kterém je operace.
V některých složitějších systémech se pro aritmetické operace používá více než jeden registr a v některých případech i speciální registry pro některé instrukce. Které jsou většinou dokumentovány, ale v jiných případech, protože jsou použity pouze v určitých pokynech, nejsou obvykle dokumentovány.
Důvodem pro použití registrů je jejich blízkost k ALU, pokud RAM paměť se používá, pak by provedení jednoduché operace trvalo mnohem déle. Druhým důvodem je to, že k provedení operace by bylo spotřebováno mnohem více energie.
S tím vším je vysvětleno, jak ALU funguje, alespoň v základních pojmech.