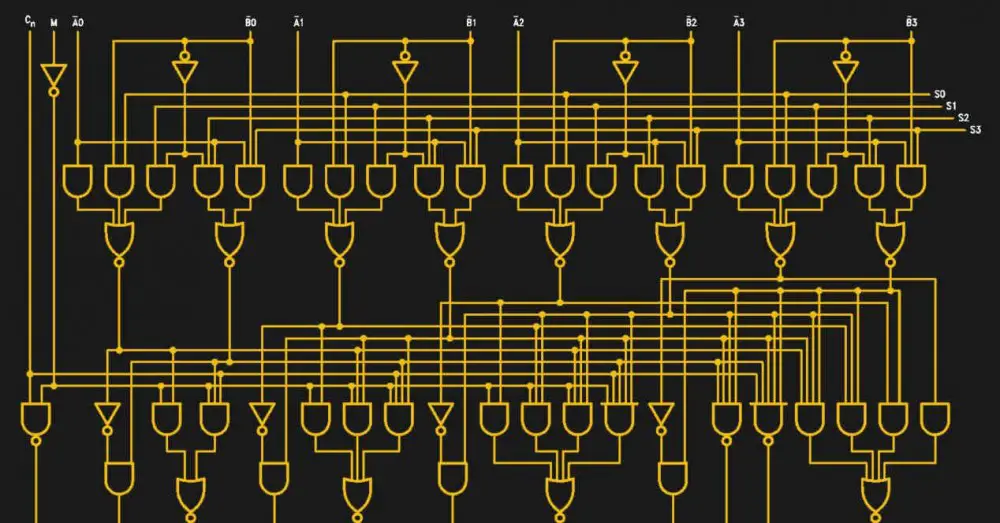
ALU 또는 스페인어로 논리 산술 단위로 알려진 단위는 CPU 또는 GPU 문자 그대로 숫자를 처리하는 역할을하므로 PC에서 초당 수십억 번 수행되는 모든 수학적 계산을 담당합니다. 그러나 어떻게 작동하며 어떤 유형이 있으며 ALU 장치의 비밀은 무엇입니까? 알아 보려면 계속 읽으십시오.
출시 된 첫 번째 ALU는 CPU의 일부가 아니라 Texas Instruments의 TTL 인터페이스가있는 7400 시리즈 칩이었습니다. 74181은 단일 칩에 통합 된 최초의 ALU였습니다. 4 비트에 불과했고 1960 년대에 다양한 미니 컴퓨터에 사용되어 컴퓨팅 분야에서 처음으로 큰 전환을 이루었습니다.
70 년대에 완전한 명령주기를 실행하기위한 모든 해당 요소와 함께 첫 번째 완전한 CPU의 구성은 분명히 칩 내부의 논리 및 산술 명령을 계산하기 위해 ALU의 통합에 의존해야했습니다.
ALU의 유형
ALU를 두 개의 다른 세분으로 나눌 수 있습니다. 첫 번째는 계산할 숫자의 유형에 따라 다르므로 정수 또는 부동 소수점으로 작동하는 경우 후자의 경우 소수로 작동하는 것에 대해 이야기합니다. 부동 소수점 연산은 정수 부분에 해당하는 숫자 비트 수와 소수 부분에 해당하는 비트 수를 나타내는 규칙을 따릅니다.
두 경우의 표준은 또한 첫 번째 숫자가 부호를 표시하는지 여부를 나타냅니다. 예를 들어 8 비트 정수의 숫자는 사용 된 형식에 따라 0에서 255 또는 -127에서 127 사이의 숫자를 나타낼 수 있습니다.
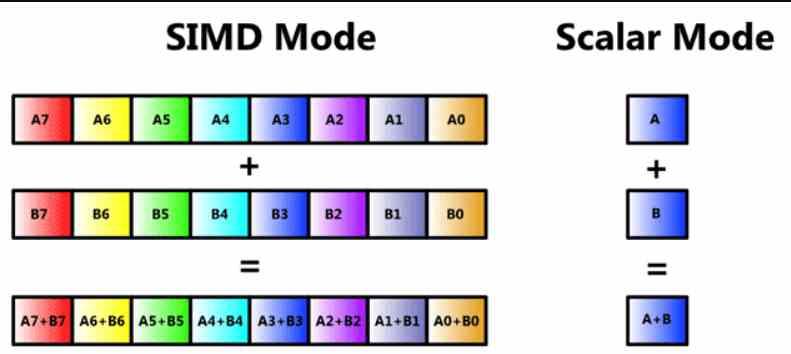
두 번째 분류는 ALU가 동시에 실행하는 데이터 및 명령어 수를 나타냅니다. 가장 간단한 형식은 연산 또는 명령어가 피연산자에 의해 수행되는 스칼라 ALU입니다. 동시에 다른 피연산자로 동일한 명령어를 수행하는 SIMD 또는 벡터 단위도 있습니다.
ALU를 사용하는 작업 유형
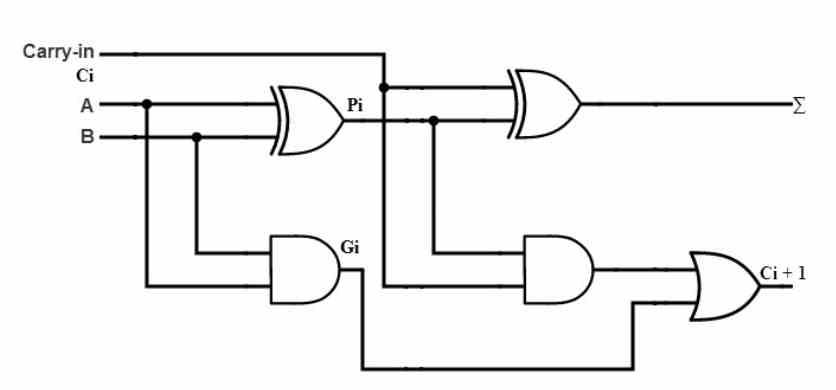
우선, 자체적으로 작동 할 수없는 ALU가 있어야하므로 수행 할 명령과 수행 할 데이터를 표시하는 제어 장치가 필요합니다. 그래서이 설명에서 우리는 ALU에 수반되는 제어 장치가 있다고 가정 할 것입니다.
CPU 또는 GPU와 같은 모든 유형의 프로세서가 이진수로 수학 연산을 수행 할 수있게 해주는 ALU입니다. 따라서 이것은 이진 계산기에 지나지 않습니다. ALU의 가장 간단한 유형으로 각각 1 비트의 두 숫자를 추가 할 수 있습니다. 이는 다음과 같은 연산입니다.
| 조작 | 결과 | 끌기 |
|---|---|---|
| 0 + 0 | 0 | 0 |
| 0 + 1 | 1 | 0 |
| 1 + 0 | 1 | 0 |
| 1 + 1 | 1 | 1 |
이것들을 보시면 OR 타입의 로직 게이트 사양이지만, 1 + 1을 더한 결과가 1이 아니라 1이기 때문에 10 + 1을 더할 때 문제가되는 문제를 발견했습니다. 특히 우리가 훨씬 더 높은 정밀도의 비트로 작업하기를 원하고 따라서 비트 수에서 훨씬 더 복잡한 ALU를 갖고 싶다면, 우리가 가지고 다니는 캐리의 1이므로 간단한 OR 게이트로는 충분하지 않다는 것을 고려해야합니다.
ALU의 이진 빼기
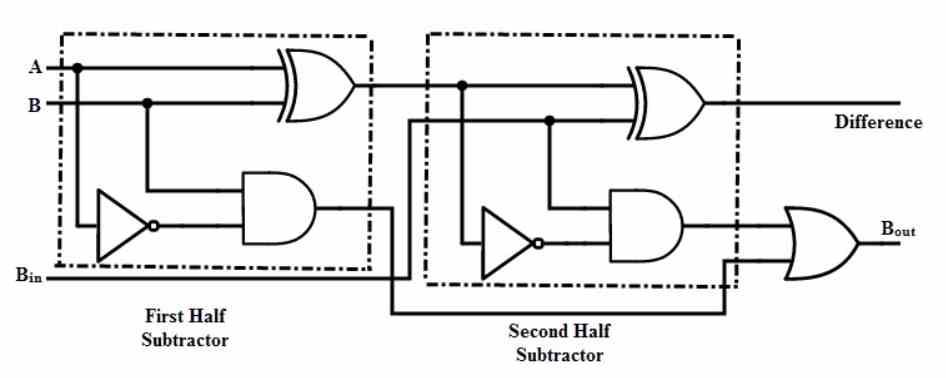
빼기 또는 빼기는 다음 공식으로 파생 될 수 있습니다.
A – B = A + 아님 (B) +1
여기서 트릭은 매우 간단합니다. 이것은 우리가 이진 정수로 작업하고 있다는 사실을 기반으로합니다. 이것은 부동 소수점 숫자에서는 작동하지 않습니다. 빼기 연산을 수행하기 위해 두 숫자를 더하는 데 사용되는 동일한 메커니즘을 사용할 수 있습니다. 우리가해야 할 일은 일련의 NOT 게이트를 통해 작동하는 두 번째 값을 반전하고 최종 결과에 1을 더하는 것입니다. 덕분에 동일한 하드웨어를 사용하여 더하기 연산을 수행하여 빼기를 수행 할 수 있습니다.
2의 거듭 제곱으로 이진 곱셈과 나눗셈
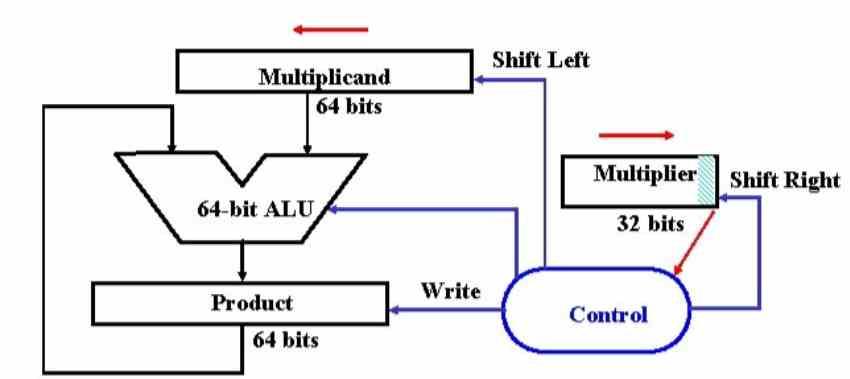
이진 시스템에서 가장 단순한 형태의 곱셈은 2의 배수로 곱하는 것입니다. 이진 시스템이기 때문에 입력 데이터가 곱하는 경우 왼쪽 또는 왼쪽으로 여러 위치 이동하는 메커니즘 만 구현하면됩니다. . 맞습니다, 우리가 나누고 있다면. 위치 수? 곱셈기 2의 거듭 제곱 인덱스에 따라 다르므로 8 ^ 2 인 3을 곱하면 3 자리를 왼쪽으로 이동해야하고 3 자리를 오른쪽으로 나누면됩니다. 이러한 이유로 ALU는 2의 배수로 곱하거나 나누는 기초가되는 비트 시프트 연산도 통합합니다.
그러나 우리가 다른 유형의 숫자를 곱하는 것에 대해 이야기한다면, 우리가 어렸을 때로 돌아가는 것이 가장 좋습니다.
2의 거듭 제곱이 아닌 숫자의 곱셈
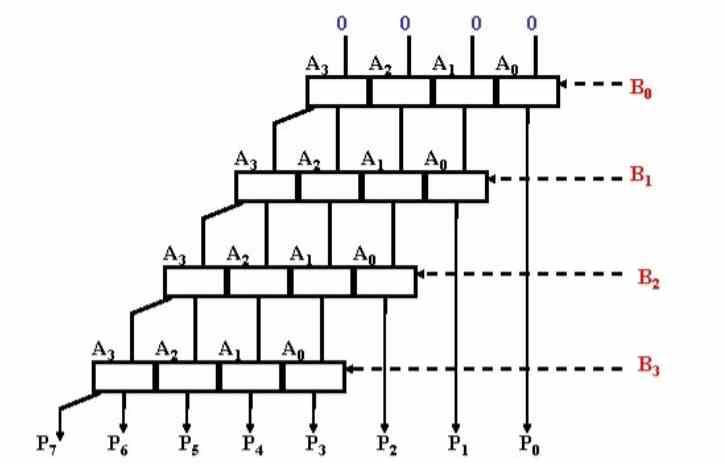
수년 동안 ALU는 매우 단순했으며 곱셈을위한 ALU가 없었기 때문에 추가 만 가능했습니다. 그때 그들은 어떻게 수행 했습니까? 글쎄, 여러 개의 연결된 합계를 실행하여 많은 사이클을 걸었습니다. 역사적 호기심으로 곱셈 단위를 가진 국내 최초의 CPU 중 하나는 인텔 8086.
우리가 어렸을 때 25 x 25를 곱하고 싶다고 가정 해 보겠습니다.
- 먼저 25 x 5를 곱하고 결과 인 125를 기록합니다.
- 두 번째로 25 x 2를 곱하면 50이됩니다. 결과를 기록하지만 한 위치를 왼쪽으로 이동합니다.
- 두 번째 숫자가 왼쪽으로 이동했기 때문에 두 숫자를 더합니다. 합계의 결과는 175가 아니라 625입니다. 이는 십진수로 25 x 25를 곱한 결과입니다.
이진법에서는 프로세스가 동일하지만이 경우 숫자 25는 11001이므로 5 비트 숫자입니다. 이진수로 11001 x 11001을 곱하고이를 위해 AND 게이트를 사용해야합니다.
- 먼저 11001 x 1 = 11001을 곱합니다.
- 둘째, 11001 x 0 = 0000을 곱하고 결과를 한 자리 왼쪽에 씁니다.
- 세 번째로 11001 x 0 = 0000을 곱하고 결과를 왼쪽에 두 자리 씁니다.
- 넷째, 11001 x 1 = 11001을 곱하고 결과를 왼쪽에 세 자리 씁니다.
- 다섯째, 11001 x 1 = 11001을 곱하고 결과를 왼쪽에 XNUMX 자리 씁니다.
- 각 작업의 위치를 고려하여 결과를 추가합니다. 01001110001
더 복잡한 수학 연산

위에서 설명한대로 나누기, 제곱근, 거듭 제곱 등과 같은 훨씬 더 복잡한 수학적 연산을 수행하는 단위를 만들 수 있습니다. 작업이 복잡할수록 분명히 더 많은 트랜지스터가 필요합니다. 실제로 각 작업마다 다른 메커니즘이 있으며 제어 장치가 실행할 작업 유형을 ALU에 알릴 때 수행하는 작업은 특정 수학적 작업에 해당 특정 메커니즘을 사용해야한다는 것을 알리는 것입니다.
중요한 것은 트랜지스터를 절약하는 것이므로 하드웨어를 재사용하기 위해 가장 복잡한 작업은 가장 단순한 작업의 연속으로 정의됩니다. 이로 인해 더 많은 수의 클록 사이클이 필요한 더 복잡한 작업이 발생합니다. 일부 설계에서는 이러한 작업이 훨씬 적은 수의 주기로, 심지어 많은 경우 단일 주기로 수행 될 수 있도록 완전한 메커니즘이 구현되지만 CPU에서는 일반적이지 않습니다.
GPU에서 사용되는 경우, 기하학에서 사용되는 삼각비와 같은 초월 적 연산을 실행하는 특수 기능 단위라는 단위 유형을 볼 수 있습니다.
ALU는 작동 할 데이터를 어디에서 얻습니까?
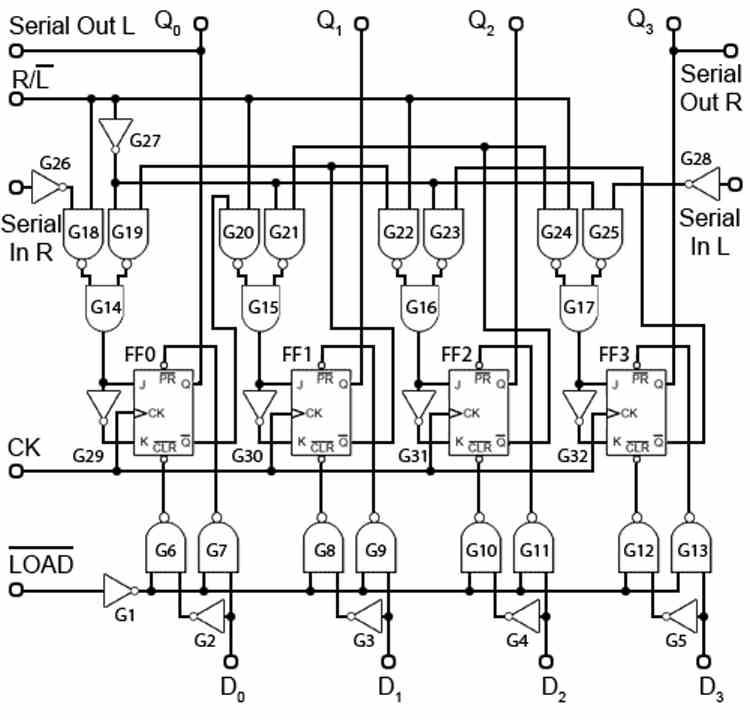
우선 ALU는 메모리의 데이터로 작동하지 않지만 작동해야하는 데이터를 캡처하고 디코딩하는 과정에서 accumulator라는 레지스터에 저장된다는 점을 염두에 두어야합니다. 작업.
일부 복잡한 시스템에서는 산술 연산에 둘 이상의 레지스터가 사용되며 경우에 따라 일부 명령어에는 특수 레지스터도 사용됩니다. 대부분의 경우 문서화되지만 다른 경우에는 특정 지침에서만 사용되기 때문에 일반적으로 문서화되지 않습니다.
레지스터를 사용하는 이유는 ALU에 근접하기 때문입니다. 램 메모리가 사용되면 간단한 작업을 수행하는 데 훨씬 더 오래 걸립니다. 다른 이유는 작업을 수행하는 데 훨씬 더 많은 에너지가 소비되기 때문입니다.
이 모든 것을 통해 ALU가 최소한 기본 용어로 작동하는 방식을 설명합니다.