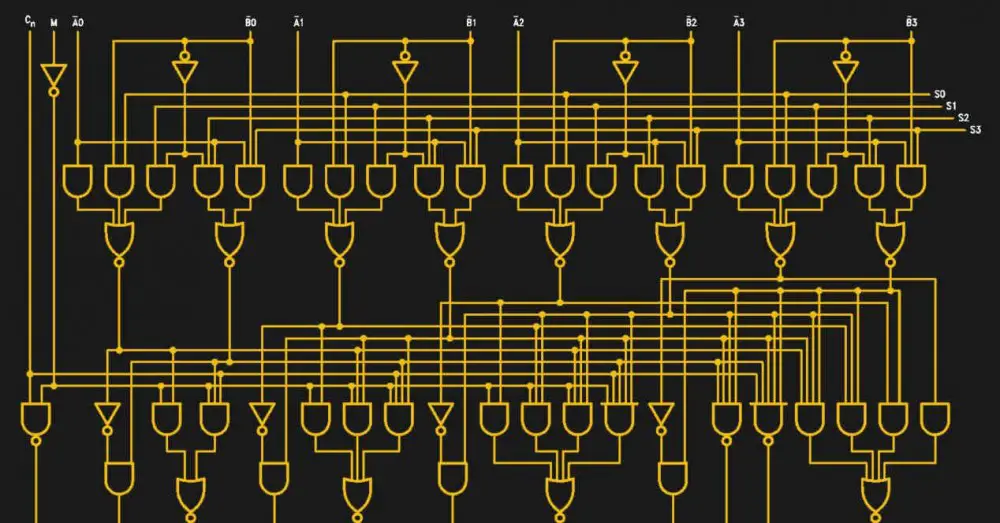
ALU eller kendt på spansk som en logikoaritmetisk enhed er enhederne inden for en CPU eller GPU der bogstaveligt talt er ansvarlige for knasende tal og derfor er ansvarlige for alle de matematiske beregninger, der udføres flere milliarder gange i sekundet på vores pc'er.Men hvordan fungerer de, hvilke typer er der, og hvad er hemmelighederne ved ALU-enheder? Læs videre for at finde ud af det.
Den første ALU, der blev frigivet, var ikke en del af en CPU, men snarere en 7400-seriechip med en TTL-grænseflade fra Texas Instruments, 74181 var den første ALU, der var integreret på en enkelt chip. Det var kun 4-bit og blev brugt i forskellige minicomputere i 1960'erne og markerede den første store overgang inden for computing.
Konstruktionen af de første komplette CPU'er i løbet af 70'erne og med alle de tilsvarende elementer til at udføre en komplet instruktionscyklus måtte naturligvis stole på integrationen af ALU'erne for at beregne de logiske og aritmetiske instruktioner inde i chippen.
Typer af ALU
Vi kan opdele ALU'erne i to forskellige underinddelinger, den første er efter typen af tal, der skal beregnes, og derfor hvis det betjenes med heltal eller med flydende punkt, hvor vi i sidstnævnte tilfælde taler om at arbejde med decimaler. Flydende punktoperationer følger en regel, der angiver, hvor mange bits af tallet, der svarer til heltalets del, og hvor mange til brøkdelen.
Standarderne angiver i begge tilfælde også, om det første tal markerer tegnet eller ej, for eksempel kan et tal i 8-bit heltal repræsentere et tal fra 0 til 255 eller fra -127 til 127 afhængigt af det anvendte format.
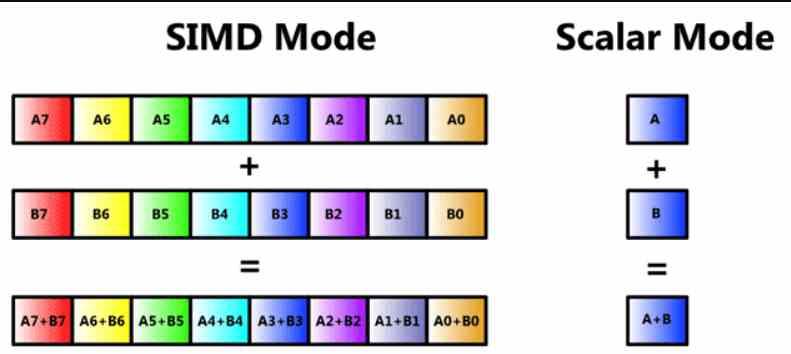
Den anden kategorisering henviser til, hvor mange data og instruktioner en ALU udfører på samme tid. Den enkleste form er den skalære ALU, hvor en operation eller instruktion udføres af operand. Vi har også SIMD- eller vektorenheder, som udfører den samme instruktion med forskellige operander på samme tid.
Typer af operationer med en ALU
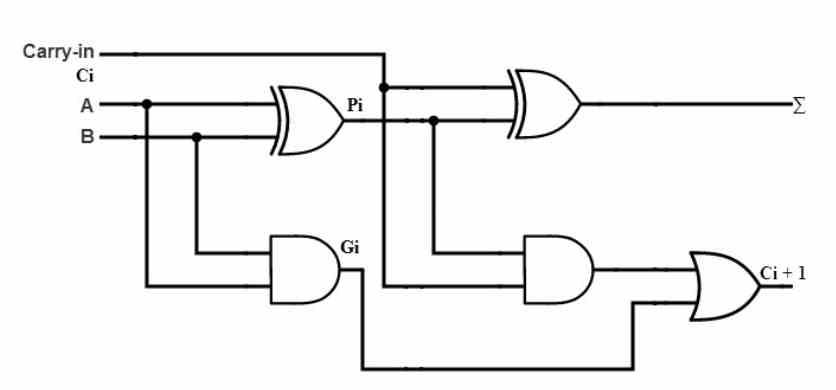
Først og fremmest skal vi have en ALU, der ikke kan fungere i sig selv, så en kontrolenhed vil være nødvendig for at angive, hvilken instruktion der skal udføres, og hvilke data der skal udføres. Så i denne forklaring antager vi, at vi har en kontrolenhed, der ledsager vores ALU.
En ALU, der tillader enhver form for processor, det være sig en CPU eller en GPU, til at udføre matematiske operationer med binære tal. Så det er intet andet end en binær lommeregner, idet den er den enkleste type ALU, der tillader tilføjelse af to tal på 1 bit hver, hvilket er en operation, der ville være som følger:
| Produktion | Resultat | haulage |
|---|---|---|
| 0 + 0 | 0 | 0 |
| 0 + 1 | 1 | 0 |
| 1 + 0 | 1 | 0 |
| 1 + 1 | 1 | 1 |
Hvis du ser på disse, er dette specifikationerne for en logisk gate af OR-typen, men vi finder et problem, der er at bære, når du tilføjer 1 + 1, da resultatet af tilføjelse af binær 1 + 1 er 10 og ikke 1. Så Vi er nødt til at tage højde for, at 1 i den bære, vi bærer, og derfor er en simpel ELLER-port ikke nok, især hvis vi vil arbejde med en meget højere præcision i bits og derfor har en meget mere kompleks ALU i antal bits.
Binær subtraktion i en ALU
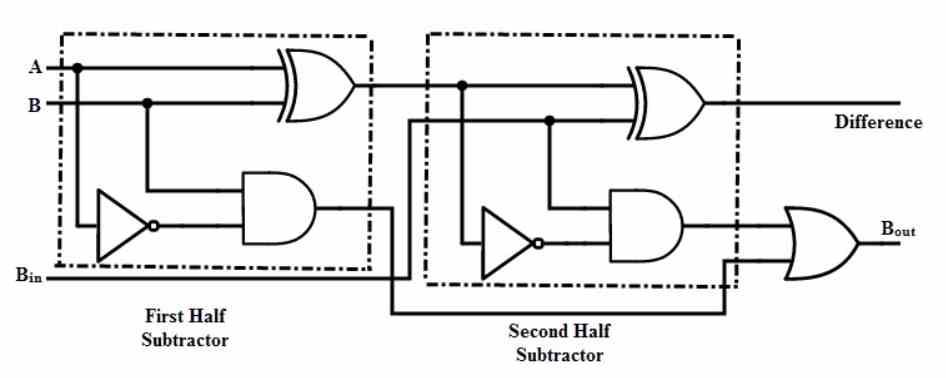
Subtraktion eller subtraktion kan afledes med følgende formel:
A - B = A + IKKE (B) +1
Tricket her er meget simpelt, det er baseret på det faktum, at vi arbejder med binære heltal. Dette fungerer ikke med flydende tal. Vi kan bruge den samme mekanisme, der bruges til at tilføje to tal til at udføre subtraktionsoperationen. Alt, hvad vi skal gøre, er at invertere værdien af det andet, der fungerer gennem en række IKKE porte og tilføje 1 til det endelige resultat. Takket være dem kan vi bruge den samme hardware til at udføre en tilføjelsesoperation for at udføre en subtraktion.
Binær multiplikation og fordeling af kræfter på 2
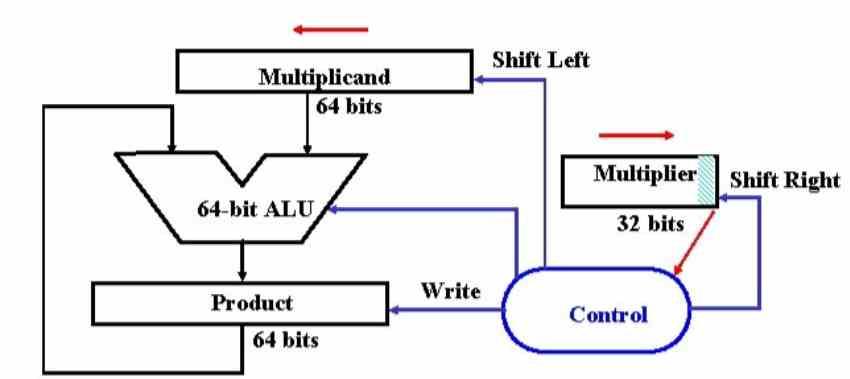
Den enkleste form for multiplikation i et binært system er multiplikation med tal multipla af 2, da det er et binært system, behøver vi kun implementere en mekanisme, hvor inputdataene forskydes flere positioner til venstre, hvis vi multiplicerer eller til venstre . rigtigt, hvis vi deler os. Antallet af stillinger? Det afhænger af effektindekset på multiplikatorens 2, så hvis vi multiplicerer med 8, hvilket er 2 ^ 3, bliver vi nødt til at skifte nummer 3-positionerne til venstre, og hvis det deler 3 positioner til højre. Det er af denne grund, at ALU'er også integrerer bit shift-operationer, som er grundlaget for at multiplicere eller dividere med multipla af 2.
Men hvis vi taler om at multiplicere andre typer numre, er det bedst at gå tilbage til, da vi var små i skolen.
Multiplikation med ikke-effekt på 2 tal
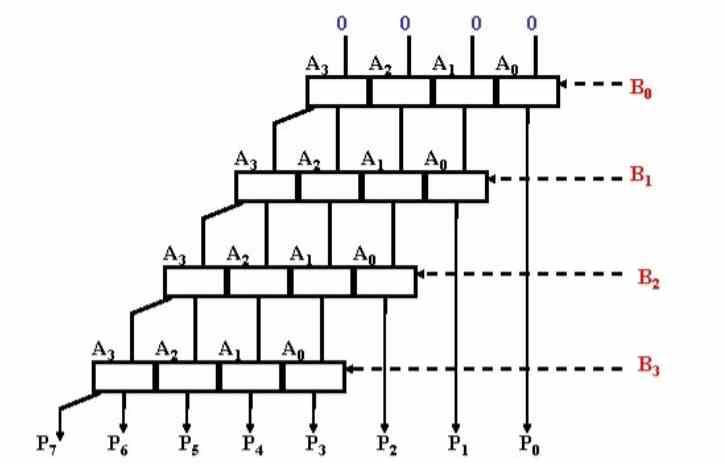
I mange år var ALU'erne meget enkle og kunne kun tilføje, da de ikke havde ALU'er beregnet til multiplikation. Hvordan klarede de sig da? Nå, udførelse af flere sammenkædede summer, der tog dem mange cyklusser. Som en historisk nysgerrighed var en af de første indenlandske CPU'er, der havde en multiplikationsenhed Intel 8086.
Antag at vi vil multiplicere 25 x 25, da vi var små, hvad vi gjorde var følgende:
- Først multiplicerer vi 25 x 5 og skriver resultatet ned, hvilket er 125.
- For det andet multiplicerer vi 25 x 2, hvilket giver os 50, og vi skriver resultatet ned, men skifter en position til venstre.
- Vi tilføjer begge tal, da det andet tal er skiftet til venstre, er resultatet af summen ikke 175, men 625, hvilket er resultatet af at multiplicere 25 x 25 i decimal.
Nå, i binær er processen den samme, men tallet 25 er i dette tilfælde 11001 og derfor et 5-bit nummer. Så binært skal vi multiplicere 11001 x 11001, og til dette bliver vi nødt til at bruge AND-porte.
- Først ganger vi 11001 x 1 = 11001
- For det andet multiplicerer vi 11001 x 0 = 0000, vi skriver resultatet et sted til venstre.
- For det tredje multiplicerer vi 11001 x 0 = 0000, vi skriver resultatet to steder til venstre.
- For det fjerde multiplicerer vi 11001 x 1 = 11001, vi skriver resultatet tre steder til venstre
- For det femte multiplicerer vi 11001 x 1 = 11001, vi skriver resultatet fire steder til venstre
- Under hensyntagen til positionen for hver operation tilføjer vi resultatet, som ikke skulle give som et resultat 01001110001
Mere komplekse matematiske operationer

Med ovenstående forklaret kan du bygge enheder til at udføre meget mere komplekse matematiske operationer såsom divisioner, kvadratrødder, magt og så videre. Jo mere kompleks operationen naturligvis vil have brug for flere transistorer. Faktisk er der for hver operation en anden mekanisme, og når styreenheden fortæller en ALU, hvilken type operation, der skal udføres, fortæller det, hvad den laver, at den skal bruge den specifikke mekanisme til den specifikke matematiske operation.
Da det vigtige er at spare på transistorer, defineres de mest komplekse operationer som en række af de enkleste for at genbruge hardwaren. Dette fører til de mere komplekse operationer, der kræver et større antal urcyklusser. Selvom der i nogle designs implementeres komplette mekanismer, der gør det muligt at udføre disse operationer i et meget mindre antal cyklusser og endda i en enkelt cyklus i mange tilfælde, men de er ikke almindelige i CPU'er.
Hvor de bruges i GPU'er, hvor vi ser en type enhed kaldet Special Function Unit, der er ansvarlig for at udføre det, vi kalder transcendentale operationer, såsom de trigonometriske forhold, der bruges i geometri.
Hvor får ALU dataene til at fungere?
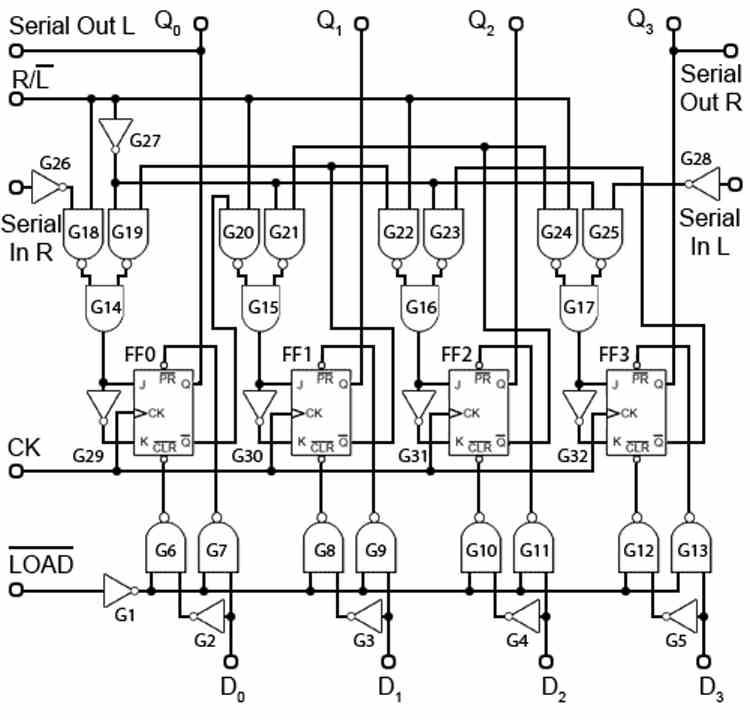
Først og fremmest skal vi huske på, at en ALU ikke fungerer med dataene i hukommelsen, men at der i processen med at indfange og afkode de data, som den skal arbejde med, lagres i et register kaldet akkumulator, hvorpå operationer.
I nogle mere komplekse systemer bruges mere end et register til aritmetiske operationer og i nogle tilfælde endda specielle registre til nogle instruktioner. Som er dokumenteret det meste af tiden, men i andre tilfælde, fordi de kun bruges i visse instruktioner, er de normalt ikke dokumenteret.
Grunden til at bruge registre er på grund af deres nærhed til ALU, hvis RAM hukommelse bruges, så vil det tage meget længere tid at udføre en simpel handling. Den anden årsag er, at der forbruges meget mere energi til at udføre en operation.
Med alt dette forklares det, hvordan en ALU fungerer, i det mindste i basale termer.